5件
白銀比とは、
概要
まず、長方形を1つ考える。長いほうの辺を半分にすると、小さい長方形ができる。この長方形が、元の長方形と相似であるようにしたときの、辺の比を白銀比という。
もっと具体的にいうと、1:√2である。この比は古くから日本の建造物に用いられている。2辺の比が白銀比であるような長方形を白銀長方形といい、印刷紙にも使われている。
作図法
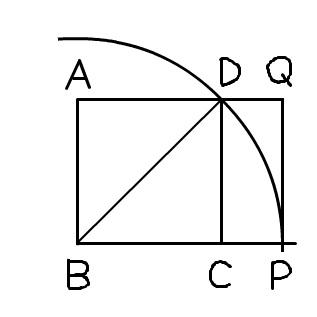
- 正方形ABCDを作図する。
- Bを中心とした、半径BDの円を描く。
- 辺BCをCのほうに延長し、2.で描いた円との交点をPとする。
- Pを通り、辺BCに垂直な直線を描く。
- 4.で描いた直線と、辺ADの延長線との交点をQとする。
- 長方形ABPQが、白銀長方形である。
証明
上記のとおり作図したとき、長方形ABPQが白銀長方形であることを示す。
Bを中心とした、半径BCの円を描く。
その円と対角線BDとの交点をEとする。
EPを結ぶ。
Eを通り、辺BCに垂直な線を描き、辺BCとの交点をP',辺ADとの交点をQ'とする。
辺BCと線分BEは長さが等しい。
対角線BDと線分BPも長さが等しい。
角CBDと角EBPは同じ。
よって、三角形BCDと三角形BEPは合同。
よって、三角形BEPは、BPを斜辺とした直角二等辺三角形である。
線分EP'は線分BPに垂直なので、三角形BEP'と三角形PEP'は合同。
よって、P'は線分BPの中点である。
したがって、長方形ABP'Q'は、長方形ABPQの長いほうの辺を二等分して得られる長方形である。・・・(1)
線分EP'と線分DCは平行なので、三角形BEP'と三角形BDCは相似。
よって、線分の長さの比で、BP':BE = BC:BDが成り立つ。
線分BE,線分BCは線分BAと長さが等しく、線分BDは線分BPと長さが等しい。
よって、BP':BA = BA:BPが成り立つ。
したがって、長方形P'BAQ'と長方形ABPQは相似。・・・(2)
別証
前述の証明は、白銀比の具体的な値を用いない証明である。しかし1:√2であることがわかれば、「ピタゴラスで一発」でだいたい通じる。ちゃんと書こうとすると次の通り。
辺ABの長さをaとする。
辺ACの長さもaなので、ピタゴラスの定理より対角線BDの長さはa√2である。
よって、線分BPの長さもa√2である。
したがって、辺ABと線分BPの長さの比は、1:√2である。
ゆえに、長方形ABP'Q'は白銀長方形である。
関連項目
- 3
- 0pt
