概要
3次方程式は、一般的にax3+bx2+cx+d=0の形で書かれる。このxをa,b,c,dの式で表すことができれば、それが「解の公式」と言える。
この公式が発表されたのは16世紀のイタリア。カルダノという数学者が自身の出版の中に記載したため、この名前がつけられている。しかし、解法については彼が独自に編み出したものではなく、先に解いていたデル・フェロやタルタリアから聞き出したものを元にしている。
式
ただし、p=(-b2+3ac)/3a2,q=(2b3-9abc+27a2d)/27a3,ω=(-1+i√3)/2,kは整数。
第2項は-p/3を第1項で割っても求められる。
pとqの式は覚えようとするとかなり複雑なので、実際に解く際には、x=y-b/3aを代入し、y3+py+q=0の形にするほうが早い、かもしれない。
例題
x3-3x2+2=0を、カルダノの公式を用いて解け。
解答
x=y+1とおくと、(y+1)3-3(y+1)2+2=0
展開して、y3-3y=0
よって、p=-3,q=0
カルダノの公式を用いると、(k=0のときの)第1項は、3√(√-1)=-i
-p/3=1より、第2項は1/(-i)=i
よって、x=-i+i+1,-ωi+ω-1i+1,-ω2i+ω-2i+1
したがって、x=1,1±√3
虚数の発見
前述した例題のように、実数解を求める際にも、計算過程で虚数が現れるのである。「負の数の平方根」については、2次方程式を解く際にも出現するが、その時代からずっと「あり得ないもの」として扱われていた。しかし、カルダノの公式によって、実数という「あり得るもの」を求めるのに「あり得ないもの」を用いるという、当時の人々には到底理解しがたい結果がもたらされた。否定的な声が多かったと思われるが、その「あり得ないもの」について今一度考えるきっかけにもつながり、現代では電気工学をはじめとした様々な分野に応用されている。
関連動画
関連項目
- 0
- 0pt
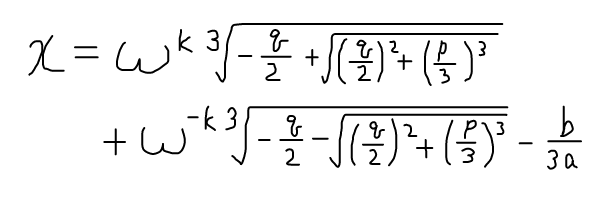




![[黒い艦これ]さよならごっこ](https://nicovideo.cdn.nimg.jp/thumbnails/35900902/35900902.31263731)

