探求のパラドックスとは、哲学者・プラトンによる対話篇『メノン』で論じられたパラドックスである。
概要
「探求する対象を知らなければ、そもそも探求できない。しかしその対象を知っていれば探求する必要がない」というパラドックス。以下の2つの背理によって成り立っている。
- 探求する対象Xを知らないのであれば、Xをどのような方法・目処で探求すればよいのかすらわからない。仮にXらしきものに到達したとしても、それが本当にXなのかを確かめるすべはない。
- 探求する対象Xを知っているのであれば、そもそもXについて探求する必要はない。
この2つの背理によって探求の必要性に疑問を投げかけているのが探求のパラドックスである。『メノン』では、「対象X」を「徳」に置き換えて論じている。
『メノン』での問答
「一辺の長さが2プースである正方形ABCD、その2倍の面積をもつ正方形の一辺の長さはいくつか」という疑問(以降、正方形の疑問)を通じ、探求のパラドックスの解消を図っている。※1プース≒1インチ、約2.54cm。
登場人物
- ソクラテス
- 哲学者。無知の知を説いており、徳について探求する自分自身も「徳とはなにかを知らない」と考えている。それにも関わらず、問答を通じて相手も徳についてわからなくさせており、メノンから「シビレエイのようだ」と揶揄されている。
- メノン
- 貴族の子息。本対話篇のタイトルにもなっている人物。ソクラテスに対して「徳は人に教えることができるのか」と尋ねたことをきっかけに、探求のパラドックスを提唱する。
- メノンの召使
- ソクラテスとの問答を通じ、正方形の疑問に実際に取り掛かる少年。幾何学の知識は最低限度しか持ち合わせていない。
本編
「徳とはなにか」についてあれこれ説を唱えるメノンだが、いずれもソクラテスによって否定されてしまう。以下の対話・問答はそこからスタートする。なお、原文からかなり省略・意訳しており、実際にはより細かく話を区切り、召使に確認をとったり考えを聞いたりしている。
「長くて読んでいられない!」という方はこちらをクリック(タップ)。
メノン(以降、メ):シビレエイもその都度近付いて来て、自身に触れる人間を痺れさせますが、私にはあなたがシビレエイのようなことをしているとしか思えません。あなたと話すまでは徳について自信のある考えを持っていたにも関わらず、話して以降は「徳がなんなのか」すらわからなくなってしまいました。
ソクラテス(以降、ソ):私に言わせてもらえば、シビレエイは自分でも痺れてしまうことはないので、その指摘には当たらない。というのも、「徳とはなにか」という難問の答えを私自身も知らず、難問にひどく苦しんでいるのは自分自身だからだ。君は私と話すまでは徳を知っていたが、私と話してからは徳について知らない人と同じような状態になってしまった。それでも私は、「徳とはなにか」を君とともに探求したいと思うのだ。
メ:それでは、ソクラテス。あなたはどんなふうに「それが何であるかも見当がつかないようなもの」を探求するのです?また、一体どのように探求の目標や目処をつけるのでしょう?さらに、たとえ望み通りのものに到達したとしても、一体どのようにしてそれが当のものであると確定できるのでしょう?
ソ:つまり君はこう言いたいのだろう?
「人間は知っていることも知らないことも探求できない。知っていることであれば探求する必要はないだろう。すでにそのことについて知り尽くしているから。また人間は知らないことであっても探求できない。なぜなら何を探求するかさえわからないからである。」
メ:私にはよくできている言説だと思うのですが……。
ソ:私にはそうは思えない。
メ:ではどの点がまずいのでしょう?
ソ:私はオルフェウス教やピュタゴラス教の信徒から次のような教えを聞いたことがある。
「人々の魂は不滅で、たとえ肉体が滅んだとしても再び現世に生まれ落ちてくるのである。だからこそ人は人生をより敬虔に過ごさなければならない。そうすれば後世でより偉大な人物に生まれ変われるからだ。」
このように魂は不滅で何度でも蘇るわけだが、そうした過程で魂は森羅万象を知り尽くしており、現世の我々は探求によってそれを想起しているに過ぎないのだ。だから先のような言説によって探求を怠ってはならないし、徳についても同様に、それが何であるのかを君と探求したいと思うのだ。
メ:わかりました。しかし私達が「学習」や「探求」と呼んでいるものは実は「想起」であるというのは、一体どういうことなのでしょう?それを示してはもらえませんか?
ソ:そうしよう。君の召使の中から私の相手を1人選んでここに呼びなさい。彼がしているのは「想起」なのか、それとも私から「学習」しているのか、よく注意して観察しなさい。
――メノンの召使がやって来る。ソクラテスは彼に幾何学の問題を出題する。
|
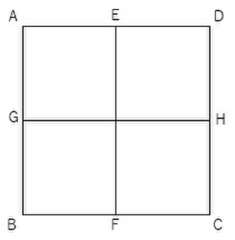
ソ:では出題しよう。ここに正方形ABCDがある。四辺はいずれも等しいし、それぞれの真ん中を通る2本の線(EF、GH)も等しい(図1)。
メノンの召使(以降、召):はい。
ソ:では一辺の長さが2プース(≒2インチ、約5.08cm)のとき、正方形ABCDの面積は何平方プースだろうか?
こう考えよう。長方形ABFEについて考えたとき、辺ABが2プースで辺BFが1プースだから、この図形は2プースを1倍した面積、つまり2平方プースとは考えられないだろうか?
召:そうなります。
ソ:さて、それでは正方形ABCDの2倍の面積を持つ正方形を作れるかな?
召:はい、作れます。
ソ:それはどのくらいの面積だろうか?
ソ:ではその正方形の1辺の長さはどのくらいだろう?
――ここで一度召使を退席させ、ソクラテスとメノンで問答する。
ソ:召使は今、8平方プースの正方形の一辺の長さについて知っていると思っている。そうだろう?
メ:ええ、そう思えます。
ソ:では、この召使は実際にその長さを知っているかい?
メ:いいえ、知りません。
ソ:それでも彼は「一辺の長さを2倍にすれば面積も2倍になる」と思い込んでいる。これから話を再開するが、この召使が想起すべきとおりの順番で想起していくから、よく見ていなさい。
ソ:再開しよう。君は「一辺の長さを2倍にすれば面積も2倍になる」という。間違いないね?
召:はい、そうです。
|
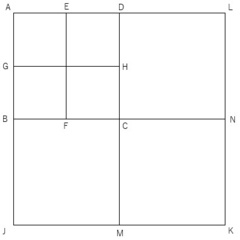
ソ:ではこうしよう。辺ABと同じ長さの線分BJを辺ABの先にくっつけると、線分AJは辺ABの2倍になる。同じような線分をあと3つ引けば、正方形ABCDの2倍の面積を持つ正方形AJKLができる(図2)、と君は主張している。
召:はい。
ソ:正方形AJKLには、元の正方形ABCDと同じ面積の正方形が4つ含まれている。そうすると正方形AJKLの面積はいくつだろうか?
召:いいえ、4倍になります。
ソ:したがって、一辺の長さを元の2倍にすると、面積は元の4倍になる。8平方プースの正方形というのは、正方形ABCD(4平方プース)より大きく、正方形AJKL(16平方プース)より小さいものではないだろうか?
召:ええ、そう思います。
ソ:そうそう、君の思うとおりに答えなさい。ということは8平方プースの正方形は、一辺の長さが辺AB(2プース)より長く、辺AJ(4プース)より短いものでなければならない。ではそのような一辺の長さはどのくらいだろうか?
召:3プースです。
|
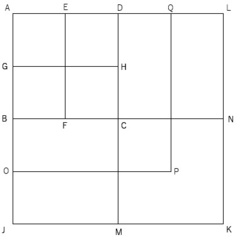
ソ:なるほど、では辺ABの先っぽに1プースの長さである線分BOをくっつけてみよう。そうすると辺AOは3プースの長さになる。同じような線分を3本引くと、正方形ABCDの2倍の面積を持つ正方形AOPQができる(図3)。そうだね?
召:はい、そう考えます。
ソ:辺AOが3プース、辺AQが3プースだから、正方形AOPQに面積はいくつだろう?
ソ:それでは一体何プースの辺から面積が8平方プースの正方形は作れるだろうか?具体的な長さでなくて、どのような線か答えるだけでもいいよ。
召:神に誓って、私はそれを知りません!
――もう一度召使を退席させ、メノンと問答する。
ソ:想起によって召使がどのような思考をたどっているか、君は気付いたかな?最初、彼は面積が8平方プースの正方形の一辺がどういう長さかを知っていると思いこんでいた。それが難問であるかも、自身がそれに悩まされるとも思いもしなかった。しかし今の彼は自分が難問に悩んでいると考えており、自分が知らないという事実を知った。彼は知っていると思いこんでいたときよりも優れた状態にあるのではなかろうか。
メ:おっしゃるとおりだと思います。
ソ:私は彼を難問で悩ませ、シビレエイのように彼を痺れさせた(わからなくさせた)わけだが、それで私は彼に何か害を与えたかい?
メ:いいえ、そんなことはありません。
ソ:それで君は、彼が難問に悩んでいると気付き、自分が知らないという事実を知るよりも前の時点で、本当は知らないのに知っていると思い込んでいる物事を探求・学習してみようと考えられるかな?
メ:いいえ、そうは思えません。
ソ:つまり、彼は痺れさせられた(わからなくさせられた)ことによって自分のためになったと。では話を再開させるが、彼が難問で悩んでいるなかから一体何を想起していくのかを考えて欲しい。また私が問うだけで彼は想起できるのか、私が彼に何かを教え示してしまっていないかを見張っていて欲しい。
――召使を呼び戻し、問答を再開する。
ソ:では再開しよう。正方形ABCDと同じ大きさの正方形を3つくっつけると、元より4倍の面積を持つ正方形AJKLができる。ここまではやったよね?
召:はい。
|
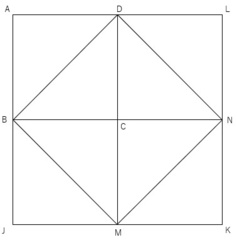
ソ:さて、点Bから点Dに向かって、正方形ABCDを二等分にするような線分が引ける。同じように他の3つの正方形でも二等分にするような等しい長さの線分が引ける(線分DN、NM、MB)。するとこの4つの線分で正方形BDNMができる(図4)。ではこの正方形BDNMの面積はいくつだろう?
召:わかりません。
ソ:4つの図形(正方形ABCD、DCNL、CMKN、BJMC)があり、4本の斜線はそれぞれ正方形を内側で二等分しているのではないかな?
召:そのとおりです。
ソ:正方形BDNMのなかに、先ほどの内側で二等分した三角形はいくつあるかな?
召:4つです。
召:2つです。
ソ:4は2の何倍かな?
召:2倍です。
召:この線(BD)です。
ソ:専門家はこのような線を「対角線」と呼んでいる。つまり君の答えは
「2倍の面積の正方形は、対角線を一辺として作ることができる」
ということかな?
召:はい、間違いありません。
――召使を退席させ、メノンとの問答を再開する。
ソ:どうだろう?彼は自分のものではないような考えを1つでも口にしただろうか?
メ:いいえ、彼が答えたのは自分の考えでした。
ソ:ほんの少し前は、彼は「2倍の面積の正方形は、対角線を一辺として作ることができる」ことを知らなかった。しかしそれでも、このような考えは元々彼の中に存在していた。したがって、当の本人が知らないことでも、その人の中には正しい考えが内在している。そうだろう?
メ:そう思います。
ソ:今はこのような考えをようやく呼び覚ましたに過ぎない。しかし何度も繰り返し問答をしていくうちに、彼はこのような考えを自分の知識として定着させることができるだろう。そうすると、誰かが彼に教えるでもなく、彼は自分自身の中から知識を再び獲得することができるのではなかろうか?そしてそれはまさしく「想起」ではないだろうか?
メ:おっしゃるとおりです。
ソ:現世で誰かから教わったわけでもなく、彼はこのような正方形の考えを持ち合わせていた。それはつまり今の生より前にそれらの考えを獲得しており、それが質問によって現世で呼び覚まされただけに過ぎない。もしも森羅万象の真理が我々の魂に内在しているのであれば、魂は不滅であろう。したがって君が今知らない(思い出していない)ことがあれば、一所懸命それを探求・想起しなければならない。なぜならそうすることで後世でより偉大な人物に生まれ変われるからだ。
メ:優れた説のように思えます。なぜそう思ったかは説明できませんが。
ソ:そうだろう。私だって理由を説明できずにそう思っているのだから。しかし、自分の知らないことを探求することはできないと考えるよりも、自分の知らないことを探求すべきであると考えるほうが、より優れた者ではなかろうか?私はできる限りそれを主張していくつもりだし、それを行動で示していくつもりだ。
メ:その言説も私には正しいように思えます。
本編の要訳
- 正方形の疑問に対して、メノンの召使は最初「4」(一辺の長さを2倍にすれば面積も2倍になる)と答えた。しかしソクラテスとの対話を通じて自身の考えが誤りであることに気付き、最終的には「2倍の面積の正方形は、対角線を一辺として作ることができる」という真理に辿り着いた。
- ソクラテスによると、人々の魂というのは輪廻転生しており、その過程ですでにありとあらゆる真理(イデア)を知り尽くしているという。しかしながらそれは人々の奥底にあって容易には取り出せないため、探求や学問を通じてそれらを想起(アナムネーシス)するのである。つまり真理は誰かから教わるような外側にあるものではなく、自分自身の力で見つけ出すような内側にあるものである。よって真理を想起するには常に自発的な探求・学問に勤しまなければならないため、探求のパラドックスは誤りである。このような思想を「想起説」という。
解説
正方形の疑問に対して、当初召使は「一辺の長さを2倍にすれば面積も2倍になる」という考えを持っていた。しかしソクラテスとの問答を通じてその考えが誤りであることに気付き、その後試行錯誤を経て「正方形ABCDの対角線の長さに等しい」という真理に辿り着いた。この成果は、ソクラテスが召使に直接教え込んで得られたものではなく、召使の自発的な気付きによってもたらされたものだ。ソクラテスが対角線を引いたのはあくまで真理への糸口を作ったに過ぎず、召使の判断能力を最大限に引き出す補助である。
このように自身の奥底にある真理を思い起こすのに探求・学習は不可欠であるから、探求のパラドックスは誤りである、とソクラテスは主張している。このような考えを「想起説」という。
ソクラテスが実演してみせたのは幾何学についての真理だったが、これは徳の真理についても同様と言える。
召使の思考変化を見ると、「知っていると思いこんでいる→問答を通じてわからなくなる(無知の知)→糸口から真理に気付く」といった順番をたどっており、これはソクラテスが好んで使っていた問答法の典型例である。自身が徳について知らないにも関わらず問答を通じて相手を惑わせたのは、決して嫌がらせの類ではなく、問答法で無知の知を自覚させつつ、相手とともにより高次の真理への糸口を探すためである。
魂が本当に輪廻転生するかはさておき、誰かから受動的に教わった物事よりも、自らが能動的に探求・学習した物事のほうが覚えがよいということであれば、大方の人々は体感的に納得行くのではなかろうか。ソクラテスはこうした自発的な学びを推奨しており、学びの営為そのものを否定しかねない探求のパラドックスは人々を堕落させるだけだと警鐘を鳴らしている。
余談
探求のパラドックスは本当に解消されたのだろうか。ここで冒頭の2つの背理を再掲する。
- 探求する対象Xを知らないのであれば、Xをどのような方法・目処で探求すればよいのかすらわからない。仮にXらしきものに到達したとしても、それが本当にXなのかを確かめるすべはない。
- 探求する対象Xを知っているのであれば、そもそもXについて探求する必要はない。
2.については解決したと言えよう。なぜならメノンの召使のようにXを知っていると思いこんでいるかもしれず、さらなる探求によって自身の考えをより磨きあげなければならないからだ。
では1.はどうだろう?仮にある程度見当をつけ、探求によってXらしきものを想起したとしても、本当にそれがXであるかは確認できない。なぜならそのXらしきものについてもまた、知っているつもりになっているだけかもしれないからである。探求の必要性については説明できたが、ある種「想起のパラドックス」と言うべきものが新たに発生してしまっている。果たして想起に終わりはあるのか、それとも終わりが無いのが想起なのだろうか。それについて探求するのもまた、一興かもしれない。
関連項目
- 7
- 0pt






