最大流問題

最大流問題とは、最大の流量を求める問題である。線型計画問題のひとつ。

概要

例えば、ある地点から他の地点に情報を送信するとする。このとき、いくつかの地点を経由し、分岐や合流をしながら情報が送られるとする。送信される過程で、一度に送ることのできる情報量の最大値がそれぞれ決まっている際、全体で一度に送信できる情報量の最大値はいくらなのか。これを考えるのが最大流問題である。最大流問題では、情報量をフロー、送信側をソース、受信側をシンクという。

フロー増加法

最大流問題を解くアルゴリズムのひとつ。

1. フローをすべて0にする。
2. 残余ネットワーク(後述)を求める。
3. 残余ネットワークにソースからシンクへつながる路がなければ、6へ飛ぶ。あれば、その中から1つ選ぶ。
4. その路の残余容量の中で最小のものを、その路の各フローに加える。既に流れている方向と逆方向にフローを加えるのは、フローを減少することを意味する。
5. 2へ戻る。
6. この時点での流れ方が、最大流である。

残余ネットワークとは

「あとどれだけフローを増加できるか」を図にしたもの。

例えば、地点Aから地点Bへ最大で5流せるとし、実際に2流れているとする。このとき、さらにフローを3だけ増やすこともできるし、流れている2をキャンセルすることもできる。この量を「残余容量」という。AからBへの残余容量は3、BからAへの残余容量は2である。残余容量をすべて求め、図にしたものが残余ネットワークである。

例

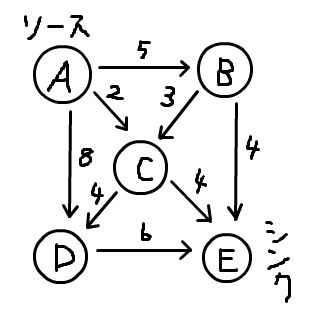
上図を例にして、最大流をフロー増加法で求める。

フローをすべて0にしたときの残余ネットワークは、上図に一致する。A→B→Eにフローを4加えると、残余ネットワークは次のとおり。

A→D→Eに6加える。

A→C→Eに2加える。

A→B→C→Eに1加える。

AからEにつながる路がないため、ループ脱出。最大流は13で、次のように流せばよいことがわかる。(流量は括弧付きで記す)

最大流最小カット定理

全体を、ソースを含む部分Sとシンクを含む部分Tの2つに分割するとき、SとTの組をカットという。Sの点からTの点に流れ込む容量の合計を、そのカットの容量という。存在しうるカットの中で容量が最小のものは、その容量と最大流が一致する。これが最大流最小カット定理である。つまり、最大流を求めることと最小カットを求めることは同等な関係にある。これは線形計画問題における双対問題であることを意味している。

前述の例でいうと、最小カットは以下の通り。

他のカットを調べても、確かに13より小さくなることはない。

関連項目

• 数学
• グラフ理論