最短経路問題

最短経路問題とは、出発点から目的地までの最短経路を求める問題である。線形計画問題のひとつ。

概要

例えば、電車を乗り継いで駅間を移動する場合、複数のルートが考えられることがある。その場合、どの線に乗るか、どの駅で乗り換えるか等で移動距離や所要時間が変化する。では、どのルートを通れば最も効率的に行けるのか。これを考えるのが最短経路問題である。最短経路問題の対象になるのは距離、時間、費用など様々あるが、ここではすべて「距離」という表現で統一する。最短経路問題で必要となる情報は、出発点、目的地、経由地、各地点のつながり(どこからどこへ直接アクセスできるか)とその距離である。

ダイクストラ法

最短経路問題を解くアルゴリズムのひとつ。

1. 未確定リスト、確定済リスト、各地点の暫定最短距離、各地点の直前に訪れる地点を記録するため、紙などを用意する。
2. すべての地点を未確定リストにリストアップする。
3. 出発点の暫定最短距離を0、その他の地点の暫定最短距離を∞とする。
4. 未確定リストが空になるか、目的地が確定済リストにあれば10へ飛ぶ。そうでなければ未確定リストの中から暫定最短距離が最も小さいものをひとつ選ぶ(これを地点aとする)。
5. 地点aを未確定リストから消去し、確定済リストに加える。
6. 地点aから直接アクセスできる地点の中で、未確定リストに載っているものをすべて見つける。
7. その各地点について、地点aの暫定最短距離と地点aからの距離を足す。
8. それが、その地点の暫定最短距離を下回っていたら、暫定最短距離を更新し、直前に訪れる地点を地点aにする。
9. 4に戻る。
10. 目的地の最終的な暫定最短距離の値が最短距離。直前に訪れる地点を出発点に到達するまで順々に巡っていけば、最短ルートがわかる。

解説

未確定リストとは、出発点からの最短距離が未確定な地点のリストのこと。確定済リストとは、最短距離が確定済みの地点のリストのこと。暫定最短距離は、出発点から確定済リストの地点のみを経由してその地点に行ったときの最短距離を表す。確定済リストの地点の暫定最短距離は、確定した最短距離である。∞であれば、確定済みリストの地点のみを経由しても行けないことを意味している。

出発点から出発点までの距離が0なのは明らかである。よって出発点は確定済リストに加え、それ以外を未確定リストにしてよい。出発点から直接アクセスできる地点をすべて見つけ、それぞれの地点について出発点からの距離を出す。これが暫定最短距離になる。それ以外の地点は、出発点から直接行けないので暫定最短距離は∞である。

ここまででループ(前項の4～9)の1巡目までが完了する。ループの1巡目までは、前項のアルゴリズムと本項の解説で違う部分があるが、結果的には同じになる。アルゴリズムで解説より回りくどい方法をとっているのは、プログラムにしたときにソースコードが短くて済むからである。

未確定リストの中で暫定最短距離が最小の地点は、他の未確定リストの地点を経由して行こうとすると、そこに行くだけで距離がかかってしまう。よって、確定済リストの地点のみを経由したほうが最短になることがここで確定する。つまり、最短距離が確定するのである。そこで、その地点を未確定リストから確定済リストに移す。

確定済リストが更新されたので、未確定リストの各地点の暫定最短距離も更新される。確定済リストには地点aが追加されただけなので、未確定リストの各地点の暫定最短距離は地点aを経由して行く場合と経由せずに行く場合のうち短いほうとなる。前者なら地点aまでの最短距離と地点aからの距離の和、後者なら(確定済リストに地点aが追加される前の)暫定最短距離となる。地点aから直接行けない場合は地点aを経由することはないため、更新されない。

前2段落の操作を、目的地の最短距離が確定するまで繰り返す。

例

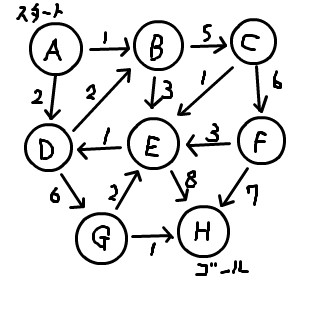右図を例にして、AからHまでの最短距離をダイクストラ法で求める。

まず、すべての地点を未確定とし、Aの暫定最短距離を0、その他の地点の暫定最短距離を∞とする。

地点	確定	最短	直前
A	未	0	-
B	未	∞	-
C	未	∞	-
D	未	∞	-
E	未	∞	-
F	未	∞	-
G	未	∞	-
H	未	∞	-

未確定な地点の中で暫定最短距離が最小なのはAなので、Aを確定済リストへ。Aから直接アクセスできる未確定な地点はBとD。0+1<∞、0+2<∞なので、BとDの暫定最短距離をそれぞれ更新する。

地点	確定	最短	直前
A	済	0	-
B	未	1	A
C	未	∞	-
D	未	2	A
E	未	∞	-
F	未	∞	-
G	未	∞	-
H	未	∞	-

未確定な地点の中で暫定最短距離が最小なのはBなので、Bを確定済リストへ。Bから直接アクセスできる未確定な地点はCとE。1+5<∞、1+3<∞なので、CとEの暫定最短距離をそれぞれ更新する。

地点	確定	最短	直前
A	済	0	-
B	済	1	A
C	未	6	B
D	未	2	A
E	未	4	B
F	未	∞	-
G	未	∞	-
H	未	∞	-

未確定な地点の中で暫定最短距離が最小なのはDなので、Dを確定済リストへ。Dから直接アクセスできる未確定な地点はG。2+6<∞なので、Gの暫定最短距離を更新する。

地点	確定	最短	直前
A	済	0	-
B	済	1	A
C	未	6	B
D	済	2	A
E	未	4	B
F	未	∞	-
G	未	8	D
H	未	∞	-

未確定な地点の中で暫定最短距離が最小なのはEなので、Eを確定済リストへ。Eから直接アクセスできる未確定な地点はH。4+8<∞なので、Hの暫定最短距離を更新する。

地点	確定	最短	直前
A	済	0	-
B	済	1	A
C	未	6	B
D	済	2	A
E	済	4	B
F	未	∞	-
G	未	8	D
H	未	12	E

未確定な地点の中で暫定最短距離が最小なのはCなので、Cを確定済リストへ。Cから直接アクセスできる未確定な地点はF。6+6<∞なので、Fの暫定最短距離を更新する。

地点	確定	最短	直前
A	済	0	-
B	済	1	A
C	済	6	B
D	済	2	A
E	済	4	B
F	未	12	C
G	未	8	D
H	未	12	E

未確定な地点の中で暫定最短距離が最小なのはGなので、Gを確定済リストへ。Gから直接アクセスできる未確定な地点はH。8+1<12なので、Hの暫定最短距離を更新する。

地点	確定	最短	直前
A	済	0	-
B	済	1	A
C	済	6	B
D	済	2	A
E	済	4	B
F	未	12	C
G	済	8	D
H	未	9	G

未確定な地点の中で暫定最短距離が最小なのはHなので、Hを確定済リストへ。Hから直接アクセスできる未確定な地点はない。

地点	確定	最短	直前
A	済	0	-
B	済	1	A
C	済	6	B
D	済	2	A
E	済	4	B
F	未	12	C
G	済	8	D
H	済	9	G

Hの最短距離が確定したが、全ての地点が確定するまで続ける。未確定な地点の中で暫定最短距離が最小なのはFなので、Fを確定済リストへ。Fから直接アクセスできる未確定な地点はない。

地点	確定	最短	直前
A	済	0	-
B	済	1	A
C	済	6	B
D	済	2	A
E	済	4	B
F	済	12	C
G	済	8	D
H	済	9	G

すべての地点が確定したのでループ脱出。ここから、AからHまでの最短距離は9で最短ルートはA→D→G→Hであることがわかる。さらに、各地点までの最短ルートが次のようになることもわかる。

関連項目

• 数学
• グラフ理論