デデキントカット

デデキントカットとは、数学の実数論において用いられる考え方である。
デデキント切断、あるいは切断とも呼ばれる。　この記事ではデデキントカットで統一する。

また、厳密な定義やこれを用いたさらなる計算等は棚上げし、「数学が苦手な人」「イマイチ理解できない人」向けに書いてる事をまず了承してほしい。

概要

デデキントカットとは

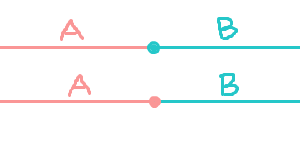
要素が小さい順番にならんだ集合Rがあるとする。
これを「集合A」と集合Aの全ての要素より大きい要素で構成された「集合B」に分ける(大きい方と小さい方の2群に分けるということ)。

この様な(A,B)をRのデデキントカットと呼ぶ。

R = A∪B, A≠∅,B≠∅ ; a∈A, b∈B ⇒ a<b

デデキントの公理

そして、Rがすべての実数の集合の時、以下のどちらかが成り立つ。これをデデキントの公理（定理）と呼ぶ。　（元とは、要素と同じ意味である。）

①Aに最大元がなく、Bに最小元がある。
②Aに最大元があり、Bに最小元がない。

別の表現をするなら数直線を2つに切ると、境目の一方は開区間、もう一方は閉区間になるということである。また別の表現をするなら数直線をx = aで切ると、 x < a, a ≤ xかx ≤ a, a < xに分かれるということである。

もうちと分かりやすく

これを「集合A」と集合Aの全ての要素より大きい要素で構成された「集合B」に分ける

↑という文面について、分かりづらい人もいるかもしれないので、少し詳しく見てみよう。

集合Aに関する言説だけを見ると、Aとして「1と2とπと、4〜5の間全部と……」という具合に、好き勝手な実数の集合を選べそうに見える。しかしながら、実際にはAは「あるところから、それより小さいもの全部」と選ばないと駄目である。なぜならば、Aの選び方に隙間があると、そこの部分は必ずB に属さなければならず、「Bの元はAのすべての元より大きい」という条件に反するからである。

例えば無限に長いロープを考えよう。このロープの全体が、実数の全体である。
Aさんには-∞側を、Bさんには+∞側を持ってもらうとして、このロープを「デデキントカット」するためには、どこか一箇所だけを切断して「Aさん側にあるものは集合A、Bさん側にあるものは集合B」という具合にするしかない。
なぜこの分割をデデキント「カット」と呼ぶかは、この例えでおおよそ理解して頂けると思う。

となると唯一議論の余地があるのが、カットしたまさにその点がどこに行くか、である。そこでロープにとても小さい点を書いて、そこを目印にロープを切るとする。点はとても小さいので、点が左右に真っ二つになる事はない。

デデキントの公理（定理）によれば、この時、以下のどちらかが成り立つ。

①点がA側になく、B側にある。
②点がA側にあり、B側にない。

何故２つに絞れるか？

先程、①か②のどちらかになる。といったが、以下の様に分かれる可能性があるのではないだろうか？

③A側に最大元があり、B側にも最小元がある。
④A側に最大元がなく、B側にも最小元がない。

最大元、最小元が共にある？

まず前提より、「集合A」と集合Aの全ての要素より大きい要素で構成された「集合B」とあるので、最大元＝最小元となる事はない。最大元αは集合Aに属しており、最小元βは集合Bに属しているので、α<βという事がわかる。

ところで、「有理数は稠密である」と言われる。稠密とは「密集している」「ぎっしり詰まっている」という意味合いがあるのだが、これはどういう意味だろうか？

1と1.1は共に有理数であるが、その間に有理数はあるだろうか？1<δ<1.1である有理数δを考えればよい。例えばδ=1.01、1.012等…
さらに間を狭めよう。1と1.000000001も共に有理数であり、間に有理数がある。同様にもっともっと間を狭めても、その間に有理数があるという事が分かる。

この様に考える事で、「有理数と有理数の間にはまだまだ無限に有理数がある」という事が分かるだろう。
これが有理数がびっしり敷き詰まってる様を表し、有理数は稠密であると言わしめる所以である。

以上の事を踏まえて最大元αと最小元βが共に存在する、となると「その間にある有理数」が実数の全順序集合Rに含まれていない事に気付く。ロープに例えると、点αと点βの2ヶ所でロープを切ると「その間のロープはどこに行ったの？」という話である。

という事で③の「A側に最大元があり、B側にも最小元がある。」は成り立たない事が分かった。

最大元、最小元が共にない？

先にロープの例を出すと、点をまず１つ打ってそこでロープ切断した結果、「点がA側にもB側にも無く、どこかへ行ってしまった」という事になるのだが、それはまず考えにくいという事を私達は知っている。

そして、数学的にこれを考えるのには少し頭をひねる必要がある。
例えば有理数の全順序集合Qを先程と同様にデデキントカットしよう。実は有理数におけるデデキントカットでは、「最大元と最小元がどちらも存在しない」は成立する。

例えば、次のようなAとBを考えてみよう。

A: 2乗すると2未満になる正の有理数、および0と負の有理数

B: 2乗すると2以上になる正の有理数

これはデデキントカットの条件を満たす取り方になっている。にもかかわらず、最大元αと最小元βは存在しない。なぜならば「2乗してちょうど2になる有理数」は存在せず、A側としては1.4,1.41,1.414,...、B側としては1.5, 1,42, 1.415...のように、その2乗が2に近付くような列をいくらでも取る事ができるからである。

しかしながら、私達は2乗するとちょうど2になる数が√2であり、それが無理数である事を知っている。そして実数全順序集合Rはその様な数も含まれている事を知っている。よって切断による数が不特定になる様な事は決してない。よって④の「A側に最大元がなく、B側にも最小元がない。」が実数の全順序集合Rのデデキントカットでは起こり得ない事が分かった。

デデキントカットが数を定義する

以上から、デデキントカット(A,B)において「Aに最大限があり、Bに最小限がない」または「Aに最大限がなく、Bに最小限がある」のどちらかしか成り立たない事を改めて確認した。
さらに、「デデキントカットをすると、最大元か最小元のどちらか一方が存在する」という事は「実数を切断する上で、１つの数が確定する」を表してる。

例えば「2でデデキントカットする」という事は「Aの全ての要素≦2,2＜Bの全ての要素」か「Aの全ての要素＜2,2≦Bの全ての要素」のどちらかが成立するという事であり、これは2が実数の数直線の中にただ１つの点として含まれているという事を示してる。これは他のあらゆる実数でも適用でき、同様に１つの実数が数直線上で１つの点と１：１で対応している。

つまり、全ての実数が僅かな隙間なく並んでおり、数直線をどこかで切れば「何かの実数」に触れてしまう。
それは実数の連続性を示してる事に他ならない。それがデデキントカットの考え方だ。

---

蛇足になるかもしれないが、先程までのロープは細かい所まで見ると例えとして不適切かもしれない。
何故ならロープは分子や原子レベルまで見ると、確かに原子と原子の間に「隙間」があり、連続とは言えないのである。

最も相応しい例として、「日の変わり目」がある。例えば時間を(A,B)とデデキントカットした様に(31日,1日)と切断したとしよう。とすれば、切断面は時間はその日の変わり目なのだが、0:00と捉えるか24:00と捉えるかでその瞬間がどちらの日に含まれるかが変わってくる。

①日の変わる瞬間が0:00ならば　…　31日が終わる時間はなく、1日の始まりは0:00である。
②日の変わる瞬間が24:00ならば…　31日が終わる時間は24:00であり、1日の始まる時間はない。

という発想ができる。同様の事がどの瞬間どの時間でも出来るので、時間というのは連続であり、あらゆる瞬間で前と後に分ける事ができる。この考え方はまさにデデキントカットだ。

また、デデキントカットで更なる問題を追及するのにε-δ論法は欠かせない。是非参考にしてほしい。

---

「実数は連続である」という今となっては当たり前の事実を、リヒャルド・デデキントやゲオルク・カントールは当時「無理数って何だよ…」と数学者が頭を抱えてる時代に「無理数論」としてまとめた。筆者はこの「今」を作る多くの偉人に感服している。

関連動画

関連商品

関連コミュニティ

関連項目

• 数学