お絵かきロジックとは (オエカキロジックとは) [単語記事]

				1		2	1	1	1
				2	4	1	1	1	1
			1	1	1	1	1	1	1	1
		1	7	1	1	1	1	1	1	7	1
	10
	2
	2
	8
1	1
1	1
	8
1	1
1	1
	8

お絵かきロジックとは、ペンシルパズルの一つである。「イラストロジック」「ののぐらむ」「ピクロス（ピクチャークロスワード）」など、さまざまな呼称がある。

概要

縦と横にある数字をもとにマス目を塗りつぶし、浮かび出るイラストや文字が何なのかを当てるパズルゲーム。具体的にどういうパズルゲームなのかは、「ルール」または「解法」の節を参照のこと。

1988年に、西尾徹也といしだのんがそれぞれ独自に創案した。西尾は雑誌『パズラー』、いしだは『社会新報』でお絵かきロジックを初公開したが、いずれも発行日が1988年 7月8日と同じだったため、「どちらが真の創案者なのか」と論争が繰り広げられた。現在は「互いにパクリや剽窃等しておらず、たまたま同時期に類似のパズルが誕生しただけ」と、概ね結論づけられている。

いしだについては、当初「推理絵」という名でパズルを寄稿していたが、初公表翌年の1989年、イギリスの新聞『サンデー・テレグラフ』紙で連載される際に「NON OGR AM」（「のんの図式」という意味）と名付けられた。それ以降、日本においても一連の作品群を「ののぐらむ」と呼ぶようになる。

知識を必要とせず理詰めで解くことができるとっつきやすさ、それから解き終わったあとも楽しめる新感覚のパズルだったことから、1993年ごろに人気が急騰。1995年にはお絵かきロジックを収録したゲーム『マリオのピクロス』が任天堂より発売され、以降シリーズ化する。

ルール

マス目の左/上の数字は、その行/列の中で連続して塗りつぶすマス（黒マス）の数のことを指す。「1」であれば1マス、「10」であれば10マスピッタリ連続して塗りつぶす。
複数の数字が並んでいる場合は、その数字の順番通りに塗りつぶさなければならない。例えば「1，3，2」と並んでいる場合、1マス，3マス，2マスの順番で塗りつぶさなければならない。
数字と数字の間は、必ず1マス以上の塗らないマス（白マス）が入る。ただし、カラーロジック(複数色を用いるお絵かきロジック)の場合、異なる色同士であれば塗らないマスを挟まなくても良い。

解法

冒頭の問題をもとに解法を説明していく。なお以下の図では黒マスを「黒背景」、白マスを「×」、すでに塗りつぶした数字を「灰色文字」で表す。また説明のため、一番左の列を「アの列」、一番上の行を「Aの行」のように書き表す。

大きな数字・端から解く

図1.　大きな数字・端から解く
			ア	イ	ウ	エ	オ	カ	キ	ク	ケ	コ
					1		2	1	1	1
					2	4	1	1	1	1
				1	1	1	1	1	1	1	1
			1	7	1	1	1	1	1	1	7	1
A		10
B		2
C		2
D		8
E	1	1
F	1	1
G		8
H	1	1
I	1	1
J		8

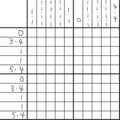
本作は縦×横=10マス×10マスの問題である。また本作での最大の数字は「10」と一致するため、Aの行はすべて塗りつぶすことができる。

また本作にはないが、まれに「0」としか書かれていない行/列がある。その場合は黒マスが一切入らないということなので、その行/列はすべて「×」と書くことができる。

次に端のJの行を見ると、本作では「10」の次に大きい「8」がある。左端から8マス塗りつぶすと仮定するとJの行ア～クまで（赤、便宜上Dの行に表示）、右端から8マス塗りつぶすと仮定するとJの行ウ～コまで（青で表示、便宜上Gの行に表示）が黒マスということになる。どちらにしろ重複するウ～クまで（紫で表示）は黒マスであることが確定するので、そこを塗りつぶすことができる（図1：Jの行）。同様に、D・Gの行もウ～クを塗りつぶすことができる。これを界隈では「右寄せ・左寄せの法則」と呼ぶ。

端で塗りつぶしたマスを手がかりに解く

図2.　端で塗りつぶしたマスを手がかりに解く
			ア	イ	ウ	エ	オ	カ	キ	ク	ケ	コ
					1		2	1	1	1
					2	4	1	1	1	1
				1	1	1	1	1	1	1	1
			1	7	1	1	1	1	1	1	7	1
A		10
B		2	×	×	×			×	×	×	×	×
C		2	×				×	×	×	×		×
D		8	×									×
E	1	1	×			×	×	×	×	×		×
F	1	1	×		×	×	×	×	×	×		×
G		8	×									×
H	1	1	×		×	×	×	×	×	×		×
I	1	1	×		×	×	×	×	×	×		×
J		8	×									×

上端・下端の黒マスを手がかりに解き進めていく。

ア・コの列を見ると、すでに1マス塗りつぶされており、数字「1」とピッタリ一致することから、他のマスはすべて白マスであることがわかる。

またカ・キ・クの列を見ると、1マスずつ計4マスが塗られており、各「1」と対応しているため、他のマスはすべて白マスであることが確定する。

エの列を見ると、Aが黒マスであることからA～Dの4マスを塗りつぶすことができる。加えてGとJはそれぞれ「1」に対応するため、他のマスはすべて白マスである。オの列も、エの列とほぼ同様に塗りつぶせる。さらにこの時点で、Bの行はすべてのマスが白か黒か確定する。

ウの列については、Dの黒マスが「2」に対応することはわかるが、CとEどちらが黒マスになるのかは不明なので保留。「2」以外の「1」についてはそれぞれ確定するので、CとE以外の未確定マスはすべて白マスであることがわかる。

仕上げ

図3.　仕上げ
			ア	イ	ウ	エ	オ	カ	キ	ク	ケ	コ
					1		2	1	1	1
					2	4	1	1	1	1
				1	1	1	1	1	1	1	1
			1	7	1	1	1	1	1	1	7	1
A		10
B		2	×	×	×			×	×	×	×	×
C		2	×	×			×	×	×	×	×	×
D		8	×									×
E	1	1	×		×	×	×	×	×	×		×
F	1	1	×		×	×	×	×	×	×		×
G		8	×									×
H	1	1	×		×	×	×	×	×	×		×
I	1	1	×		×	×	×	×	×	×		×
J		8	×									×

ここまで来ると、本作の8割のマスが確定しており、正解が何であるかもおおよそ見当がつくのではなかろうか。

Cの行について、まずケは黒マスではない。ケが黒マスだと数字が「2」だけしかないのと矛盾するし、そもそも隣り合うク・コが白マスと確定しているからである。エの黒マスが「2」に対応し、かつオが白マスであることから、ウが黒マスでイが白マスであることがわかる。これにより、さきほど検討したウの列のCとEどちらが黒マスなのかも判明した。

またD・G・Jの行を見ると、ア・コが白マスであり、かつ黒マス・未確定マスの数が「8」に対応することから、それぞれイとケを塗りつぶせばいいことがわかる。

あとはイ・ケの列の「7」の分を塗りつぶせば…？

答え

図4.　答え
			ア	イ	ウ	エ	オ	カ	キ	ク	ケ	コ
					1		2	1	1	1
					2	4	1	1	1	1
				1	1	1	1	1	1	1	1
			1	7	1	1	1	1	1	1	7	1
A		10
B		2
C		2
D		8
E	1	1
F	1	1
G		8
H	1	1
I	1	1
J		8

無事完成！漢数字の「百」、大百科の「百」が浮かび出た！！！なお見栄えのため、白マスの「×」は取り除いてある。

本作はルール説明を兼ねているので、10×10=100 マスと比較的小さく、かつ簡単で解きやすい問題だったが、専門誌や専門サイトではよりサイズが大きくて難しい問題が取り揃えてある。興味が湧いた方はぜひ購読ないし閲覧してみてはいかがだろうか。

主な専門誌・専門サイト

専門誌

カッコ内は出版社名。雑誌によって問題の大きさ・難易度、懸賞、現れてくるイラストの傾向に違いがあるので、実際に書店で手にとって確認するといいだろう。

お絵かきタイム（マイウェイ出版）
ロジックメイト（マガジン・マガジン）
- ロジックメイト Mini
スーパーペイントロジック（アイア出版）
- リトルペイントロジックBEST
ロジックパラダイス（学研出版）
- ロジックパラダイスミニ
- 難問ロジックコレクション
- イラストロジックベスト・オブ・ベスト　名作・傑作セレクト

専門サイト

基本無料で問題を解くことができるサイト。近年はスマートフォンアプリでもお絵かきロジックを扱ったものがあるので、各アプリストアで確認するのもよし。

商標

ちなみに、「お絵かきロジック」「イラストロジック」「ピクロス」などのメジャーな呼称は、いずれも既に商標登録されてしまっている。よって、関連する何かを作成して有料で販売しようと考える人はこれらの商標に抵触しないような配慮が必要である。

「お絵かきロジック」：世界文化ホールディングス
「イラストロジック」：日本文芸社（雑誌区分において）、コナミデジタルエンタテインメント（コンピューターゲームその他多数の商品・サービスの区分において）
「ピクロス」：任天堂、日本ゼトック（薬剤・衛生材料などの区分において）、東京ネオプリント（織物、布などの区分において）

お絵カキコ

画像をクリック（タップ）すると、元のお絵カキコへ行くことができる（そちらで見たほうがより鮮明に映る）。ただしリンク先でスクロールすると答えが掲載されているので、自力で解く場合は注意が必要である。

お絵かきロジック単語

概要

ルール