34件
平方根とは、累乗根の一種。ある数に対して「2乗してその数になる」ような数である。
概要
面積がわかっている正方形があるとする。この正方形の1辺の長さを求めるにはどうすればよいか。正方形の面積は、1辺の長さを2乗すれば求めることができる。よって、この逆の対応を考えればよい。つまり、2乗して面積の値になる数を求めればよいのである。このときの、面積から1辺の長さへの対応が(正の)平方根なのである。
定義と性質
aの平方根とは、b2 = aを満たすbのことである。
正の数の平方根は実数に2つ(正負に1つずつ)、0の平方根は0のみ、負の数の平方根は実数には存在しない。
a≧0に対し、aの0以上の平方根を√aと書く。(テキストではこのような表現になるが、実際はaの真上まで横棒を延ばす)平方根と√の意味が混同されやすいので注意。
a,b≧0に対し、√(a2) = |a|,√a×√b = √(ab)
代表的な値
10以下の整数の平方根には、次のような語呂合わせがよく知られている。しかし、実際に使う際は電卓で計算するだろうし、学校の計算問題に出たときでもここまで覚える必要はないであろう。整数との大小関係とか、√2,√3,√5の小数第3位あたりまで覚えておけばおｋ。
√2 = 1.41421356…(一夜一夜に一見頃)
√3 = 1.7320508…(人並みにおごれや)
√5 = 2.2360679…(富士山麓オウム鳴く)
√6 = 2.4494897…(煮よよく弱くな)
√7 = 2.64575…(菜に虫いない)
√8 = 2.828427…(ニヤニヤ呼ぶな)
√10 = 3.16227766… (三色に並ぶ)
ちなみに、この語呂合わせから、ケチな人間を√3と呼んだり、√5の値は上九一色村の事件を予言していたとか、おっと、誰か来たようだ。
求め方
電卓を使う
計算尺を使う
定規とコンパスを使う
- 平方根を求めたい数の長さの線分をとり、PQとする。
- 線分PQをQのほうに1だけ延長して、端点をRとする。
- 線分PRの中点Oを求める。
- 点Oを中心に半径OPの円を描く。
- 点Qを通る、線分PRの垂線を引く。
- 垂線と円Oとの交点のひとつをSとする。
- 線分QSの長さが、線分PQの長さの正の平方根である。
証明
PS,RSを結ぶ。線分PRは円Oの直径なので、角PSRは直角。線分QSは線分PRの垂線なので、角PQSも直角。
角SPQと角RPSは同じなので、三角形SPQと三角形RPSは相似。
同様にして、三角形RSQと三角形RPSも相似。
よって、三角形SPQと三角形RSQは相似。
したがって、辺の長さの比はPQ:QS = QS:QR
QR = 1より、線分PQの長さは、線分QSの長さの2乗。
よって、線分QSの長さは、線分PQの長さの平方根。
紙と鉛筆だけを使う
「開平法」の記事を参照。
複素数の平方根
平方根が実数で存在するのは0以上の実数だけである。しかし、複素数の範囲で考えれば、負の数に限らずいかなる複素数でも平方根が存在する。負の数の平方根は純虚数、虚数の平方根は純虚数でない虚数である。虚数には正負や大小関係がないため、√という表現が使われることは少ない。あったとしても「平方根のひとつ」という意味にすぎず、ある数を一意的に表しているのではない。ただし、±√と書かれた場合は、「ふたつの平方根」という意味になるため、2つの数を一意的に表していることになる。
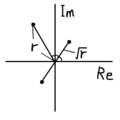
複素数を極形式でr∠θ(=reiθ)と書いた場合、その平方根は±√r∠(θ/2)となる。記号だけでは何を言ってるかわからない人もいるかもしれないので、詳しく書くと、
- 座標平面を用意する。
- 平方根を求めたい数の実部をx座標、虚部をy座標にとる。
- 2.でとった点と原点を結ぶ。
- x軸の正の方向と、3.で求めた線分とのなす角を2等分する。
- 3.で求めた線分の長さの正の平方根を求める。
- 4.で求めた2等分線上に、原点から5.の長さだけ離れている点を求める。
- 6.で求めた点と原点に関して対称な点をとる。
- 6.と7.で求めた点それぞれについて、x座標を実部、y座標を虚部とする複素数を求める。
関連動画
関連項目
- 3
- 0pt
