(有)未来検索ブラジルが運営するあらゆる言葉についての記事を閲覧・編集したり、コメントをしたりするサイトです。

単語記事: 4次元

編集 Tweet

4次元とは、次元が4つあるもののことである。

概要

空間内の点の位置を表す際に、直線上なら1つの数、平面上なら2つの数、3次元空間内なら3つの数で表現できる。こういった、「空間内の点をいくつの数で表現できるか」を次元という。4次元では、点の位置を表す際に4つの数を必要としており、3次元空間にさらに1つの座標軸が加わったものとも言える。長さの軸が4つある空間も4次元であり、複素数2つの組も、(実数上では)4次元となる。

概念

4次元が、なぜ3次元空間に時間を加えたものであるかを考える場合、1次元から3次元までの次元の成り立ちを考えると楽である。

次元なしは、ただの点（移動できない）。
1次元は、点と点を直線で結ぶ（X軸への移動）。
2次元は、1次元同士を直線で結ぶ（X軸への移動を有する状態での、Y軸への移動）。
3次元は、2次元同士を直線で結ぶ（XY軸への移動を有する状態での、Z軸への移動）。
4次元は、3次元同士を直線で結ぶ（XYZ軸への移動を有した状態での、なんちゃら軸への移動）。
この直線上の移動を3次元から見た場合、「時間」のように見える。

つまり、次元構造上では「時間」は実在しないとも言える。

4次元で言う「時間」を、3次元では知覚できない。
なぜなら、私たちが知っている「時間」とは、
脳に記憶された3次元の過去と現在を比較した差異と、
物理現象によって変化（劣化）した状態を組み合わせて導き出している概念に過ぎないのである。

その状態は、あたかも過去から未来へ進むように見え、それが私たちが知る「時間」となる。

物理学における4次元

物理学では、3次元空間と時間軸を合わせた、いわゆる時空を4次元と言う。単に「4次元」と言った場合に時空を意味していることが多い。古典力学では時間と空間を独立したものとして考えていたが、相対性理論では時間と空間が互いに影響し合うミンコフスキー時空で考える。

フィクションにおける4次元

フィクションでは、入れ物の見た目の大きさを明らかにオーバーする量が収納されている際に「4次元」と表現されることがある。これはドラえもんの四次元ポケットの影響であろう。

多胞体

多面体の4次元バージョン。3次元の多面体を複数貼り合わせることによって作られる。正多面体の4次元バージョンを正多胞体という。すべて合同な正多面体から構成され、かつ各頂点に同じ数の正多面体が集まる多胞体のことである。

以下、正多胞体について列挙する。

正五胞体: 正四面体の4次元バージョン。4次元正単体ともいう。正四面体の各頂点からの長さが、すべて1辺の長さになるように点を1つだけとって、線で結んだもの。正四面体を5個貼り合わせたものであり、10本の辺、10枚の正三角形をもつ。
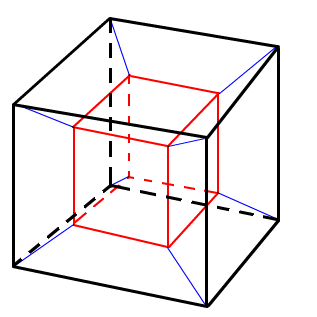
正八胞体: 立方体の4次元バージョン。4次元超立方体ともいう。2つの立方体を平行に、対応する頂点が立方体に対して垂直に、かつ距離が1辺の長さになるように配置し、線で結んだもの。立方体を8個貼り合わせたものであり、32本の辺、24枚の正方形をもつ。
正十六胞体: 正八面体の4次元バージョン。4次元正軸体ともいう。正八面体の両側に、各頂点からの距離がすべて1辺の長さになるようにそれぞれ点をとり、線で結んだもの。正四面体を16個貼り合わせたものであり、24本の辺、32枚の正三角形をもつ。
正二十四胞体: 4次元ならではの図形であり、対応する3次元の正多面体はない。正八面体を24個貼り合わせたものであり、96本の辺、96枚の正三角形をもつ。
正百二十胞体: 正十二面体の4次元バージョン。正十二面体を120個貼り合わせたものであり、1200本の辺、720枚の正五角形をもつ。
正六百胞体: 正二十面体の4次元バージョン。正四面体を600個貼り合わせたものであり、720本の辺、1200枚の正三角形をもつ。

投影図

4次元の図形を理解する方法のひとつとして、3次元への投影がある。イメージとしては、4次元の図形に光を当て、3次元のスクリーンに映す、といった感じ。投影の仕方は様々あるが、ここでは2種類の方法について述べる。ひとつは、平行な光を当てること。もうひとつは、1点から放射状の光を当てることである。

前者の方法では図形の大まかなイメージがしやすいが、本来交わらない面が交わってしまう。後者の方法では辺や面の間のつながりを保つことができるが、元の図形とはかけ離れた形になってしまう。4次元方向の奥行きは、後者の方法では中心との距離に対応し、光源から遠いものほど、3次元に射影したときに中心に近い位置になる。形が入れ子構造になっているのはそのため。

以下に挙げる図では、単独で載っているものは後者の方法をとっている。2つ載っているものは前者、後者の順であり、辺の色は対応している。お絵カキコは2次元なので、厳密には3次元投影図をさらに2次元に投影したものである(2次元への投影の仕方は前者の方法に従う)。

尚、実際の4次元の図形は、すべての頂点、辺、面、多面体が外側にある。辺の長さはすべて等しく、構成する面や多面体はすべて合同である。

注意：以下の図は、描いた人(＝当記事初版～第6版編集者)の憶測を含みます。正確な図である保証はありません。

正五胞体

超立方体

正十六胞体

正二十四胞体

宿題

長さの等しいマッチ棒を10本使って、マッチ棒1本を1辺とする正三角形を10個作れ。

4次元について語るスレ

59 ：ななしのよっしん：2012/02/07(火) 21:26:05 ID: 3pkhaTe0Iz: >>50
数学の先生が言うには、
ここは3.5次元で、なぜ.5かと言うと
4次元は時間を自由に移動できる。しかし今生きている世界は時間は一方的に進むだけで自由に動かすことが出来ないから。
ってことらしいよ。
60 ：ななしのよっしん：2012/02/17(金) 23:11:15 ID: lyydV+rmAe: 平面を動く点はそこを通過する立体を線として見るのか？
だとすれば俺らが4次元のものが通過する所を見たらどう見えるんだ？
61 ：ななしのよっしん：2012/03/02(金) 07:36:25 ID: YPBdMbtI86: >>60
想像もつかないが、昔見たＳＦホラー小説で「4次元は中に入れる合わせ鏡のような世界」という表現があった。
その話によると4次元に迷い込むと肉体が分断、分裂し、それぞれの意識を共用出来るようになるという設定だった。

ちなみにオチは4次元に長く居過ぎたため、分断状態で3次元に戻ったら、肉体がバラバラになって死亡するという話。
4次元怖ェ・・・
62 ：ななしのよっしん：2012/03/02(金) 07:56:37 ID: 2v2RpDrA88: うちの大学の教授が『時間は存在しない派』なのでここの記事やスレの内容は違和感あるな。
教授曰く『時間の存在を明確にするのは悪魔の証明に等しい』だそうだ。

例えば右から左に移動する際の連続した動きが時間の証明とするなら
それはテレビの中は動いているように見えても、テレビ本体は動いていない。つまり4次元側からすると俺らの動きは止まって見えるので、時間自体も向こうからすると無いことになるらしい。
63 ：ななしのよっしん：2012/03/02(金) 09:56:55 ID: IZwY4XYzmt: そりゃそうだ
低次元からは高次元を「理解」することは出来ても「認識」することは出来ない
認識できるのは常に自分が存在する次元よりも低い次元だけ
64 ：ななしのよっしん：2012/03/08(木) 01:00:43 ID: H/LDHtcuHv: 点と点を結べば直線、つまり一段階上の次元に到達する事ができるけど、直線を点と点に戻す事はできないんじゃね？（単に分断してもそれは細かい直線になる）
同じように、三次元と三次元を結べば（時間軸を加える）四次元になるけど、四次元を分断しても（時間軸を取り除く・逆行する）三次元にはならない・・・

だから時間は戻らないものである。とかどうかね。
65 ：ななしのよっしん：2012/03/08(木) 07:28:36 ID: auTbH+cdLS: >>64
線を分断して線になるなら、軸を除いたことにはならないんでは？
次元を減らすなら、線は点にならなきゃいけないわけで。
66 ：ななしのよっしん：2012/03/23(金) 15:51:04 ID: ojhHPZgt6/: 直線を点に戻すのは理論上可能だよ
始点から終点まで隙間無く点を敷き詰めればいい
ただし「点は長さを持たない」ので、実際に敷き詰めることは不可能
だから「始点から終点までのどこからでも点を取り出せる状態」という概念的な扱いになる
67 ：ななしのよっしん：2012/05/12(土) 22:47:08 ID: bhI+TlphK5: 皆次元次元って言う時に時間も含めて言ってるみたいだけど辞書で調べたらあくまでも空間だけってなってた。だからこの世界は3次元空間+1次元時間って考えるのがぴったりだと思ってる。物体の見え方は立体だし、時間は進む一方で巻き戻したり出来ないもんね。
68 ：ななしのよっしん：2012/05/12(土) 22:53:44 ID: bhI+TlphK5: 自分が思うに、距離→面積→体積と来たらその体積(3次元の物体)の移動は上下左右前後それぞれどの方向に動かす(引き延ばす)としても3次元の物体のままだから内側か外側に引き延ばすしか無いと思うんだ。簡単に言うと物体をその形のまま、同じ中点で内側か外側にに動かすって事。

ページトップへ戻る